嘿,未来的房产投资大师!你是否曾因为高估或低估房产价值而错失良机或踩过坑?是否想过,如果能科学预测房价走势,你的投资决策会有多么精准,资产增值会有多么轻松?今天,我们就要一起探索如何用机器学习中最经典的算法——线性回归来避开投资陷阱,实现房产投资的稳健增值。
不过别担心,我们不会用复杂的数学公式把你吓跑。相反,我们会用一个你我都熟悉的例子——房价预测——来逐步解释线性回归的每个关键概念,让你轻松掌握这个避免踩坑、促进资产增值的实用工具。准备好了吗?那就系好安全带,我们的AI房价预测之旅即将开始!
1. 从数据开始:收集我们的房价信息
任何成功的房产投资都始于对市场数据的深入理解。在机器学习中,第一步同样是获取高质量的数据。假设我们收集了以下北京房价的数据集(这是简化后的真实数据样例):
| 面积(平方米) | 卧室数量 | 学区评分(1-10) | 房龄(年) | 距离市中心(公里) | 房价(万元) |
|---|---|---|---|---|---|
| 140 | 3 | 8 | 15 | 5 | 465 |
| 90 | 2 | 6 | 40 | 3 | 320 |
| 160 | 4 | 9 | 5 | 8 | 560 |
| 80 | 2 | 5 | 25 | 12 | 215 |
| 180 | 5 | 7 | 10 | 1 | 610 |
| 120 | 3 | 8 | 12 | 2 | 445 |
看到了吗?我们有几个可能影响房价的特征(自变量):房屋面积、卧室数量、学区评分、房龄以及距离市中心的距离。而我们想要预测的目标变量是房价。
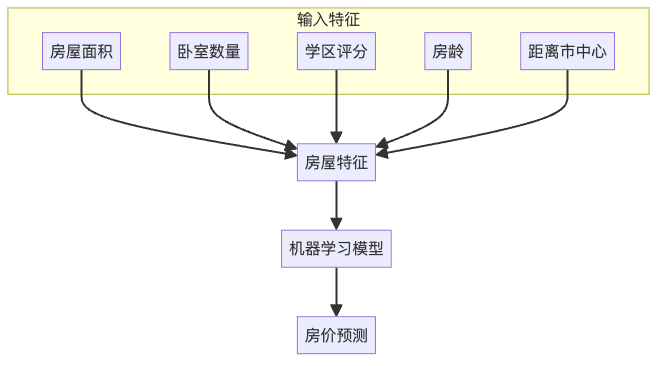
2. 理解线性回归:画一条最佳拟合线
单变量线性回归:只考虑房屋面积
为了简化我们的入门理解,让我们先只考虑一个特征:房屋面积。在这种情况下,我们假设房价只与房屋面积有关:
房价 = θ₀ + θ₁ × 房屋面积其中:
- θ₀ 是截距,可以理解为”基础房价”
- θ₁ 是斜率,表示”每增加1平方米,房价增加多少万元”
如果我们把数据点绘制在图表上,并尝试用一条直线拟合,可能会看到这样的情况:
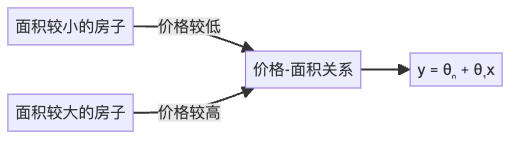
多变量线性回归:全面考虑所有特征
现实中,房价受多种因素影响。这就需要我们使用多变量线性回归:
房价 = θ₀ + θ₁ × 房屋面积 + θ₂ × 卧室数量 + θ₃ × 学区评分 + θ₄ × 房龄 + θ₅ × 距离市中心在这个方程中:
- θ₀ 仍然是基础房价
- θ₁ 是每增加1平方米,房价的增加值
- θ₂ 是每增加一个卧室,房价的增加值
- θ₃ 是学区评分每提高1分,房价的增加值
- θ₄ 是房龄每增加1年,房价的增加值(可能是负值,因为房子越老可能价值越低)
- θ₅ 是距离市中心每增加1公里,房价的变化值(通常是负值,因为越远房价越低)
3. 特征工程:让数据更好地工作
在实际应用中,我们通常需要对数据进行预处理和转换,这被称为特征工程。
特征缩放
注意到我们的特征单位差异很大:面积是平方米(可能达到几百),而学区评分只有1-10。这种差异会导致模型训练困难。我们可以使用标准化或归一化方法进行特征缩放:
# 标准化示例
面积_标准化 = (面积 - 面积均值) / 面积标准差例如,假设面积的均值是128.33平方米,标准差是37.64平方米,那么140平方米的标准化值为:
(140 – 128.33) / 37.64 ≈ 0.31
这样所有特征的尺度就变得相近了,有助于模型更快更好地收敛。
处理非线性关系
有时,特征与房价之间可能存在非线性关系。例如,房龄与房价的关系可能不是线性的:太新或太旧的房子都可能价格较高(新房因为新,老房可能因为历史价值)。
为了处理这种情况,我们可以添加多项式特征:
房价 = θ₀ + θ₁ × 房屋面积 + ... + θ₆ × 房龄² + ...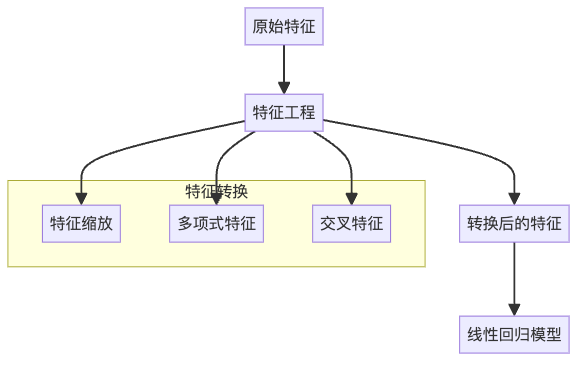
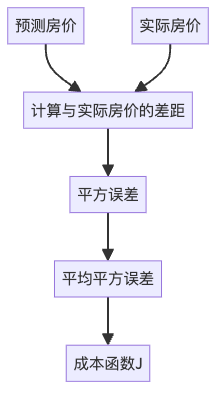
4. 成本函数:衡量预测的准确性
现在,我们需要一个方法来评估我们的模型预测得有多准确。在线性回归中,我们使用均方误差(Mean Squared Error, MSE)作为成本函数:
J(θ) = (1/2m) × Σ(预测房价 - 实际房价)²其中,m是样本数量(在我们的例子中是6)。
假设我们的初始模型参数随机设定为:θ₀ = 70, θ₁ = 1.5(只考虑房屋面积),那么:
- 第一个房子的预测价格:70 + 1.5 × 140 = 280万元(实际是465万元)
- 平方误差:(280 – 465)² = 34225
我们对所有房子进行这样的计算,然后取平均值,就得到了成本函数的值。我们的目标是找到使这个值最小的参数θ。
5. 梯度下降:找到最佳参数
现在,我们需要找到能够最小化成本函数的参数θ。这就是梯度下降算法的用武之地。
想象你在一个碗状的山谷中,你的目标是到达山谷的最低点。梯度下降就像是你看了一下周围的斜率,然后朝着下降最快的方向走一步,不断重复直到到达谷底。
在房价预测中,梯度下降会这样更新参数:
θⱼ := θⱼ - α × (1/m) × Σ(预测房价 - 实际房价) × 特征j的值其中:
- α是学习率,控制每一步的大小
- m是样本数量
- 特征j的值是对应特征的数值(例如,对于θ₁,特征是房屋面积)
举例:如果某一步θ₁ = 1.5,学习率α = 0.01,我们计算出梯度是-3.5,那么新的θ₁ = 1.5 – 0.01 × (-3.5) = 1.535。

批量梯度下降 vs 随机梯度下降
在我们的房价预测案例中:
- 批量梯度下降:每次更新参数时使用所有6个房屋样本
- 随机梯度下降:每次随机选一个房屋样本更新参数
- 小批量梯度下降:每次选择2-3个房屋样本更新参数
对于我们这个小数据集,批量梯度下降是合适的。但如果你有成千上万的房屋数据,随机或小批量梯度下降会更高效。
6. 正规方程:一步到位找最优解
对于规模不太大的房价数据集,我们还可以使用正规方程直接计算出最优参数,无需迭代:
θ = (X^T X)^(-1) X^T y其中:
- X是特征矩阵(每行是一个房屋样本,每列是一个特征)
- y是目标向量(所有房屋的实际价格)
正规方程的优势在于一步到位,不需要选择学习率,也不需要多次迭代。但当特征数量很多时,矩阵求逆的计算成本会很高。
7. 模型评估:我们的预测有多准确?投资决策有多可靠?
训练完模型后,我们需要评估它的性能,确保它能为你的投资决策提供可靠参考。假设我们经过训练得到的模型是:
房价 = 100 + 2.5 × 房屋面积 + 20 × 卧室数量 + 25 × 学区评分 - 1.0 × 房龄 - 12 × 距离市中心我们可以解释这个模型的投资洞察:
- 基础房价是100万元
- 每增加1平方米,房价增加2.5万元(面积是影响价格的重要因素)
- 每增加一个卧室,房价增加20万元(家庭型住宅通常更具投资价值)
- 学区评分每提高1分,房价增加25万元(学区是增值潜力的重要指标)
- 房子每老一年,房价减少1.0万元(新房通常更保值)
- 距离市中心每远1公里,房价减少12万元(位置仍然是房产的关键要素)
这种可解释性不仅是线性回归的一大优势,更是帮助你做出明智投资决策的关键!
使用这个模型,我们可以计算每个房屋样本的预测价格,并与实际价格比较:
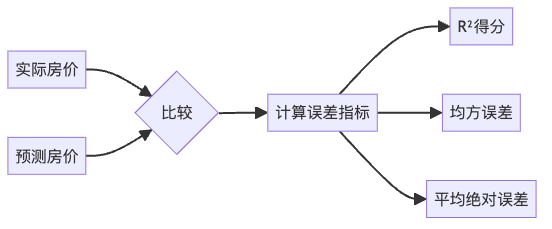
常见的评估指标包括:
- 均方误差(MSE):预测与实际值差的平方的平均值
- R²得分:表示模型解释的方差比例,越接近1越好
- 平均绝对误差(MAE):预测与实际值差的绝对值的平均值
8. 模型应用:预测新房屋的价格,避免投资踩坑
现在我们有了训练好的模型,可以用它来预测新房屋的价格,帮助你避免投资决策中的常见陷阱。假设你正在考虑购买这样一套房子:
面积: 150平方米
卧室数量: 3
学区评分: 7
房龄: 8年
距离市中心: 4公里房产中介告诉你这套房子值680万元,但你的线性回归模型给出的预测是:
预测房价 = 100 + 2.5 × 150 + 20 × 3 + 25 × 7 - 1.0 × 8 - 12 × 4
= 100 + 375 + 60 + 175 - 8 - 48
= 654万元看到了吗?这个简单的模型帮你发现了潜在的26万元溢价!通过这种方式,你可以更加客观地评估房产价值,避免因情绪化决策而踩坑,为资产增值打下坚实基础。
9. 线性回归在房价预测中的局限性
虽然线性回归简单易用,但在房价预测中也有一些局限:
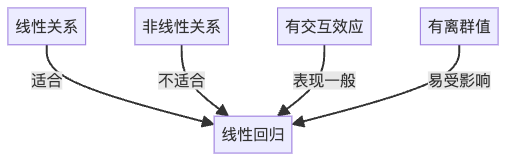
非线性关系
房价与某些特征可能存在非线性关系。例如,学区评分从9分到10分的房价增长,可能远大于从1分到2分的增长。
特征间的交互
某些特征可能相互影响。例如,大面积的房子在学区好的地方可能价格特别高,这种交互效应线性回归难以捕捉。
离群值的影响
如果数据中有一栋异常昂贵的豪宅,它可能会极大地影响我们的模型。
10. 进阶:提升你的房产投资决策模型
如果你希望进一步提高预测准确度,将线性回归打造成更强大的资产增值工具,可以尝试以下改进:
- 加入更多特征:如装修等级、车库大小、周边设施等,越全面的信息会带来越精准的预测
- 特征变换:尝试对某些特征取对数或平方,捕捉非线性关系,理解房价的复杂影响因素
- 正则化:使用岭回归(Ridge)或Lasso回归防止过拟合,让你的模型在新数据上表现更稳定
- 尝试其他模型:随着经验增长,你可以尝试决策树、随机森林或神经网络等更复杂的模型
这些进阶技巧能帮助你构建更精准的模型,为你的房产投资决策提供更可靠的参考,从而更有效地避免踩坑,实现资产的稳健增值。
结语:从线性回归到房产投资高手
恭喜你!你已经了解了如何使用线性回归来预测房价,从数据收集到模型评估的完整过程。掌握这个技能,你将能够:
- 避免买房踩坑:不再盲目相信中介的报价,而是用数据说话
- 发现低估房产:找出市场上被低估的房产,抓住投资机会
- 预测增值潜力:评估不同区域的房产增值潜力,做出更明智的长期投资
- 优化投资组合:基于客观分析而非主观感受调整你的房产投资组合
下次当朋友问你:”你觉得这房子值多少钱?”,你可以自豪地说:”等我用我的线性回归模型计算一下!”——而且你的建议可能会帮他们省下或赚到数十万元。
记住,即使是最复杂的AI系统,也是建立在像线性回归这样的基础算法之上的。掌握了这些基础,你不仅拥有了AI世界的钥匙,更获得了在房产市场中脱颖而出,实现资产稳健增值的强大工具!

