技术吧

归一化还是标准化？如何为你的数据选择最佳缩放方法

为什么你的模型需要”身高均等”？

想象一下，如果你在篮球队里同时安排了姚明（2.29米）和”小土豆”姜山（1.65米）一起打球，结果会怎样？显然，姚明会”主宰”比赛节奏。机器学习算法中的特征也是如此，不同量级的特征若不加处理，”身高优势”明显的特征就会霸占算法的”注意力”。

这就是为什么我们需要特征缩放(Feature Scaling)——让所有特征在同一个”身高标准”下竞争！

特征缩放：模型训练前的”身体检查”

在机器学习中，特征缩放就像运动员参赛前的体检，确保所有”选手”处于相同的起跑线上。它有以下重要性：

  1. 避免”巨人主宰比赛”：如果你的数据中有些特征值域很大（比如房价：几十万到几百万），有些很小（比如房间数：1-10），不缩放的话，大值域特征会”喧宾夺主”。
  2. 加速”跑步”收敛：梯度下降算法就像是在山坡上寻找最低点的盲人，如果地形高低不平（特征尺度不一），他会走很多冤枉路。特征缩放让这位盲人在更”均匀”的地形上搜索，能更快找到目标。
  3. 距离计算的”公平竞争”：想象KNN算法就是找”邻居”的过程，如果不缩放，那么在计算距离时，体重100kg的特征比身高1.8m的特征影响要大得多，这显然不公平！

举个例子：如果你的数据包含股票价格（2000-4000元）和利率（1.5%-3%），不缩放的话，股票价格的微小波动都会掩盖利率变化带来的影响。

归一化：让所有特征”手拉手站一排”

归一化(Normalization)的目标很简单：把所有特征的值都缩放到0到1之间，就像让不同身高的人蹲下或踮脚，最终都在同一水平线上。

归一化公式（Min-Max方法）

!图2：Min-Max归一化将数据压缩到[0,1]区间

这个公式做了什么？很简单：

  • 首先找出特征的最小值和最大值
  • 然后让每个值减去最小值（平移到0开始）
  • 最后除以极差（最大值-最小值），让范围刚好是1

何时使用归一化？

归一化就像是给不同身高的选手分配统一的”标准身高”，最适合以下场景：

  1. 数据分布不明确或不遵循任何特定分布时
  2. 深度学习的最爱：神经网络通常喜欢接收0-1范围内的数据（就像图像像素值从0-255归一化到0-1）
  3. 限定输出范围的算法，比如某些需要概率输入的模型

用Python实现归一化

from sklearn.preprocessing import MinMaxScaler
import numpy as np

# 假设有身高(cm)和体重(kg)两个特征
data = np.array([[180, 85], [165, 65], [190, 95], [175, 75]])

# 创建归一化器
scaler = MinMaxScaler()

# 应用归一化
normalized_data = scaler.fit_transform(data)
print("归一化后的数据:\n", normalized_data)
# 输出结果中，所有值都会在0到1之间

标准化：让特征们遵循”正态分布法则”

标准化(Standardization)则是另一种思路：不是限制值的范围，而是调整数据的统计属性，使得均值为0，标准差为1。

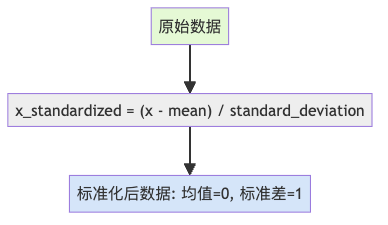
标准化的妙处

标准化后的数据就像是一群经过特殊训练的运动员，他们的平均水平是0，表现的波动程度是1。这样做有很多好处：

  1. 处理异常值的能手：归一化会被极端值搞得晕头转向，而标准化则能更好地处理这些”离群”选手
  2. 正态分布的好朋友：如果你的数据本来就接近正态分布，标准化后会更加”正态”
  3. 统计学家的最爱：很多统计模型假设数据是标准正态分布的，标准化满足这一前提

什么时候用标准化？

标准化就像是给运动员分配”表现分”而不是”排名”，最适合以下场景：

  1. 数据服从或接近正态分布时
  2. 存在异常值时（归一化会被异常值带偏）
  3. 使用涉及协方差的算法时，如PCA、SVM

用Python实现标准化

from sklearn.preprocessing import StandardScaler
import numpy as np

# 同样的身高体重数据
data = np.array([[180, 85], [165, 65], [190, 95], [175, 75]])

# 创建标准化器
scaler = StandardScaler()

# 应用标准化
standardized_data = scaler.fit_transform(data)
print("标准化后的数据:\n", standardized_data)
# 输出结果中，每个特征的均值接近0，标准差接近1

什么时候可以”逃课”？——不需要缩放的场景

并非所有算法都需要特征缩放。有些算法天生”公平”，不会偏袒任何特征：

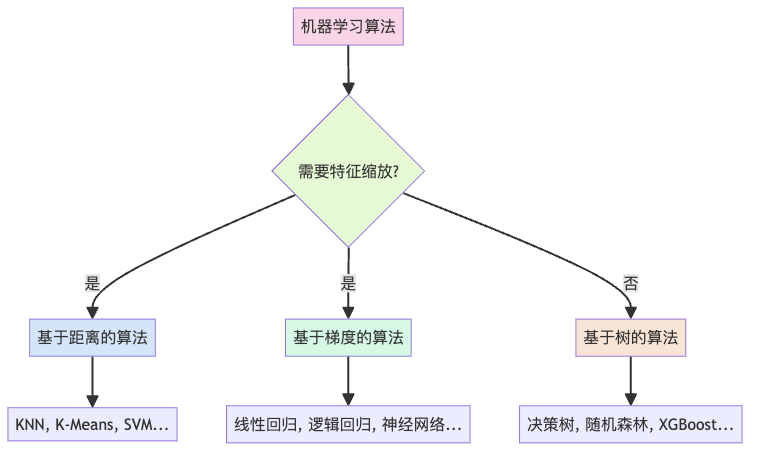
以下算法通常可以”免考”：

  1. 决策树及其家族：决策树、随机森林、XGBoost等基于树的算法不关心特征的绝对大小，它们只关心数据的排序或分割点
  2. 基于计数的算法：如朴素贝叶斯

不过，对于KNN、K-Means这类基于距离的算法，虽然技术上可以不缩放，但缩放后效果通常更好（就像虽然篮球比赛中矮个子也能投篮，但调整篮框高度会更公平）。

如何选择：归一化 vs 标准化

选择归一化还是标准化，就像选择西装还是休闲装，没有绝对的对错，要看”场合”：

归一化 (Normalization)标准化 (Standardization)
✅ 数据分布不明确时✅ 数据近似正态分布时
✅ 神经网络、深度学习模型✅ 存在异常值时
✅ 需要0-1输出的算法✅ PCA、SVM等需要方差信息的算法
❌ 存在很多异常值时❌ 需要限定范围的特征时

记住，没有”放之四海而皆准”的规则，最好的方法是：两种都试试，看哪种表现更好！

总结：特征缩放的艺术

特征缩放就像是在为机器学习模型”定制西装”，让每个特征都能完美合身。无论是归一化的”统一制服”，还是标准化的”量身定做”，目标都是让模型训练更高效、结果更准确。

最后的建议：

  1. 当不确定时，优先尝试标准化
  2. 对模型进行超参数调优时，不要忘记特征缩放方法也是一个可调参数
  3. 记得在测试数据上使用与训练数据相同的缩放参数

掌握了特征缩放，你的模型就像穿上了”隐形斗篷”，能够透过数据表象，看到真正的规律！

Post Views: 11

jsb